top of page
Apr 15, 20143 min read

The Beautiful Beta Functions: In Raw Python!

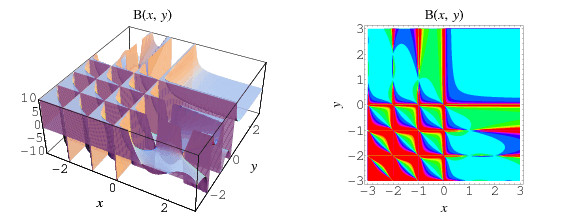
                                          Plots of Complete Beta Functions


For almost a week I have been trying very very hard to bend the computer to code for the incomplete Beta function in Python. Let me show you guys how I finally achieved it using only the most basic of Python functionality, namely, importing only math routine. The reason why I have been busting myself for this is that it (along with gamma functions) is among the foundations of many probability distributions. Once you get through these special functions, the rest of statistical computing will be only about translating from mathematics to code. And this is my sole motivation for this. Hence, I will only discuss the maths of it only superficially. I have used some useful resources to learn and code beta function (please see below: Further reading/Resources).

Complete Beta Function:

Complete Beta function can be defined in terms of gamma function as such:

Proof: for

, given

is an integer, one can write

for two of such functions, one can write

Pass the polar coordinates;

and this becomes

remember

from above. Hence,

change variable

so

and

giving,

if we define Beta function in terms of Gamma function like

then from what we have seen above,

To code the complete beta function we can use the functonality of Python math library (the only library that I ever use!). This, I think is not too much of a dependency. Sometime later, I would write a new code for log-gamma and gamma functions. Till then this short but cool code for complete beta would suffice. Lets use both math.gamma() and math.lgamma() functions (implementations of gamma and log-gamma functions respectively in math lib of python)

import math

def beta_1(a,b):
    
    '''uses gamma function or inbuilt math.gamma() to compute values of beta function'''
    
    beta = math.gamma(a)*math.gamma(b)/math.gamma(a+b)
    return beta

We can also compute complete beta function using log-gamma function. In most of resources, including ‘Numerical Recipes in C’ I have seen log-gamma being used to compute values of beta function.

import math


def beta_2(a,b):
    
    '''uses log-gamma function or inbuilt math.lgamma() to compute values of beta function'''
    
    beta = math.exp(math.lgamma(a) + math.lgamma(b) - math.lgamma(a+b))
    return beta

Incomplete Beta Function:

Incomplete Beta function was what took me so long to code. incomplete beta function can be defined as:

and the regularized beta function is closely related to both incomplete and complete beta function. We will see later in my future posts how this regularized function keeps popping up in probability theory.


import math 

def incompbeta(a, b, x):
    
    ''' incompbeta(a,b,x) evaluates incomplete beta function, here a, b > 0 and 0 <= x <= 1. This function requires contfractbeta(a,b,x, ITMAX = 200) 
    (Code translated from: Numerical Recipes in C.)'''
    
    if (x == 0):
        return 0;
    elif (x == 1):
        return 1;
    else:
        lbeta = math.lgamma(a+b) - math.lgamma(a) - math.lgamma(b) + a * math.log(x) + b * math.log(1-x)
        if (x < (a+1) / (a+b+2)):
            return math.exp(lbeta) * contfractbeta(a, b, x) / a;
        else:
            return 1 - math.exp(lbeta) * contfractbeta(b, a, 1-x) / b;

As you guys might have noted above that the function incompbeta(a,b,x) requires betacontfract(a,b,x, ITMAX), here is the code. Follow the resources below to read in detail about continued fraction method of computing incomplete beta.

import math

def contfractbeta(a,b,x, ITMAX = 200):
    
    """ contfractbeta() evaluates the continued fraction form of the incomplete Beta function; incompbeta().  
    (Code translated from: Numerical Recipes in C.)"""
    
    EPS = 3.0e-7
    bm = az = am = 1.0
    qab = a+b
    qap = a+1.0
    qam = a-1.0
    bz = 1.0-qab*x/qap
    
    for i in range(ITMAX+1):
        em = float(i+1)
        tem = em + em
        d = em*(b-em)*x/((qam+tem)*(a+tem))
        ap = az + d*am
        bp = bz+d*bm
        d = -(a+em)*(qab+em)*x/((qap+tem)*(a+tem))
        app = ap+d*az
        bpp = bp+d*bz
        aold = az
        am = ap/bpp
        bm = bp/bpp
        az = app/bpp
        bz = 1.0
        if (abs(az-aold)<(EPS*abs(az))):
            return az
        
    print 'a or b too large or given ITMAX too small for computing incomplete beta function.'
Python Functions Implemented in this Post beta_1(a,b): uses gamma function or inbuilt math.gamma() to compute values of beta function beta_2(a,b): uses log-gamma function or inbuilt math.lgamma() to compute values of beta function incompbeta(a, b, x): incompbeta(a,b,x) evaluates incomplete beta function, for a, b > 0 and 0 <= x <= 1. This function requires contfractbeta(a,b,x, ITMAX = 200) contfractbeta(a,b,x, ITMAX = 200): evaluates the continued fraction form of the incomplete Beta function; incompbeta().

Further Reading/Resources:

3 views0 comments

Comments

bottom of page