Advanced Correlation & Covariance Analysis II: Analyzing Large Datasets in Python
- Ayub Shoaib
- Dec 15, 2013
- 8 min read
In my last post I demonstrated how to perform covariance and correlation analysis properly(i.e with all the glitz and glam of decision theory). In this post I am going to show you guys, how to do it like a real pro! .. and as you have guessed… with all the python code built from scratch 😉
Real data analysis situations and real data are different from fabricated or ‘generated’ data in two important ways. Firstly, because of advent of social media and embeded systems etc. the real data sets are LARGE! Secondly, real data stes are un-clean. This means that to use the data to make inferences, one has to modify it. This branch of data science is popularly refered to as ‘data munging’. I am, however, only going to address the enormity of datasets here. I will develop code to use the protocol, I developed in last posts, and make it feasible for large dataset analysis. In the next post (hopefully 🙂 ) I will address this problem of data munging for correlation and covariance analysis. And I will use an elegant algorithm to clean the missing values and customize length of variables for an ‘automated’ correlation and covariance analysis.
In this post I introduce code that will make correlation and covariance analaysis of large datasets easy to perform. At the heart of this code is the function corcovmatrix(). This function returns a full correlation and covariance analysis along with probable and standard errors and p-values as a .csv file or text. A full analysis means all varaibles are combanitorically analysed with each other and a full report is generated as a .csv file or text. This function takes a conacatanated parent list or lists within a list. Still didn’t get it? see the example below. Remember to keep the first element of each element list to be a header string. I have used 5 variables and a a list of length 20 to keep the analysis clutter free and appreciatible.
Following code snippet shows how to construct a parent list for large data set analysis.
'here is an example of conacatanated parent list. each element is a list and first element of each list is a string type or the header. '
plist = [
['X',1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20],
['Y',20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1],
['Z',33,34,35,36,37,38,39,40,41,42,43,49,55,78,98,112,220,420,433,434],
['P',444,556,6678,432,345,231,222,341,4436,234,443,678,9996,453,221,421,223,98,2,213],
['Q',1,2,3,4,5,6,7,8,9,0,4,22,33,3,4,55,56,6,7,234],
['R',1,0,0,1,0,0,0,0,1,1,0,0,1,0,1,0,0,1,1,0]
]
I have also implemented another function concnest(). This takes infinite lists as argments and binds them all as a parent list which could be used as an argument of corcovmatrix().
#################################################################
def concnest(*lists):
'''This function takes in multiple lists as arguments ('*' denotes multiple arguments can be given to the function) and returns a concatanated and nested parent list that contains entered lists as elements. 1st element of 1st list can be indexed as list[0][0].'''
nested_list = list(lists)
return nested_list
###############################################################
And finally our star of the day corrcovmatrix() function:
################################################################
def corcovmatrix(parentlist):
''' this function takes a concatanated parent list (lists within a list) as an argument and returns a full correlation and covariance analysis along with probable and standard errors and p-values as a .csv file. A full analysis means all varaibles are combanitorically analysed with each other and a full report is generated as a .csv file or text'''
truelist = parentlist
csv_header = [' variables', ' Coefficent(r)', ' covariance', ' Probable Error', ' Standard Error', ' lower limit of rho(p)', ' upper limit of rho(p)', ' range of rho(p)', ' significance', ' P-value' , ' Df' ]
headerlist = []
n = 0
for i in truelist:
headerlist.append(truelist[n][0])
del truelist[n][0] # proper way of indexing list within a list is this ..
n = n + 1
lst1 = []
n = 0
for i in truelist[:len(truelist)-1]:
lst1.append(newcor(n,n+1,truelist,headerlist))
n = n + 1
lst2 = []
for i in range(len(truelist)-2):
j = len(truelist)-2
while j >= 0:
lst2.append(newcor(-1,j,truelist,headerlist))
j = j - 1
del truelist[-1]
del headerlist[-1]
final_header = ','.join(csv_header)
final_list = ''.join(lst1+lst2)
print(final_header)
print(final_list)
Because I didn't want to write more code than necessary and I wanted to stick with lowest level python possible (for paedagogical purposes), I have used codes from the previous two posts. For this I needed to code a unique binder function to go with the basic stat code in previous posts and the new corcovmatrix() function. This binder function is newcorr(arg1,arg2,truelist, headerlist). It takes 4 arguments. 'arg1' and 'arg2' are ints and they refer to elements of concatanated list between which a correlation is required. 'truelist' is that parent list. 'headerlist' is the list of headers of all elements. The function returns a comma-seperated-string with values of 'variables being correlated', 'correlation coefficient' , 'covariance', 'Probable Error', ' Standard Error', ' lower limit of rho(p)', ' upper limit of rho(p)', ' range of rho(p)', ' significance', ' P-value' , ' Df'
###############################################################
def newcor(arg1,arg2,truelist, headerlist):
''' This function is implemented so that, I don't have to re-write corr() function (Please refer to earlier posts). it takes 4 arguments. 'arg1' and 'arg2' are ints and they refer to elements of concatanated list between which a correlation is required. 'truelist' is that parent list. 'headerlist' is the list of headers of all elements. The function returns a comma-seperated-string with values of 'variables being correlated', 'correlation coefficient' , 'covariance', 'Probable Error', ' Standard Error', ' lower limit of rho(p)', ' upper limit of rho(p)', ' range of rho(p)', ' significance', ' P-value' , ' Df' '''
m_true = truelist[arg1]
n_true = truelist[arg2]
m_header = headerlist[arg1]
n_header = headerlist[arg2]
newcor_var = PE(corr(truelist[arg1],truelist[arg2]),len(truelist[arg1]))
pvalue = p_val(len(truelist[arg1]),corr(truelist[arg1],truelist[arg2]))
return str(m_header) +' VS '+ str(n_header) +', '+ str(corr(m_true,n_true)) + ', ' + str(cov(m_true,n_true)) + ', ' + str(newcor_var) + ', ' + pvalue + '\n'
################################################################
The output will be a csv format as follows:
you can save it as .csv format file and open it with msexcel or export as other versions:
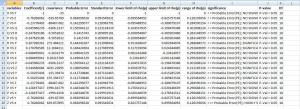
As I always keep the code as low level as possible, following is all the code you need. This code can also be downloaded here.
################################################################
import math
################################################################
def mean(arg1):
m = float(sum(arg1))
o = float(len(arg1))
p = m/o
return p
################################################################
def variance(arg1):
## Formula for Variance is = 1/N-1 . Sum (x_i - X)^2 ___ OR ___ [Sum (x_i - X)^2] / N-1 ##
# Calculating 'X' a.k.a 'mean' of the sample...
var2 = mean(arg1)
# Calculating (x-i - X)^2 ..
n = 0
lst = []
for i in arg1[:]:
var = arg1[n] - var2
n = n + 1
lst.append(var**2)
# Calculating final expression ...
variance = sum(lst) / (len(arg1) - 1)
# Returning the value of function..
return variance
################################################################
def sd(arg1):
sd = math.sqrt(variance(arg1))
return sd
################################################################
def cov(arg1, arg2):
##Formula for covariance is = 1/1-N . Sum (x_i - X)(y_i - Y) ___ OR ___ [Sum (x_i - X)(y_i - Y)] / N-1 ##
# error messages...
if len(arg1) != len(arg2):
print('Error: Lengths of variables to be correlated must be equal')
#Calculating X and Y = means
mean_x = mean(arg1)
mean_y = mean(arg2)
# Calculating (x_i - X)... for i in vector 'x'
mu = []
n = 0
for i in arg1:
var_a = arg1[n] - mean_x
mu.append(var_a)
n = n + 1
# Calculating (y_i - Y)... for i in vector 'y'
nu = []
n = 0
for i in arg2:
var_b = arg2[n] - mean_y
nu.append(var_b)
n = n + 1
# Calculating the product --> (x_i - X)(y_i - Y)...
n = 0
lst = []
for i in nu:
var4 = nu[n] * mu[n]
lst.append(var4)
n = n + 1
# Sum(x_i - X)(y_i - Y)
var5 = sum(lst)
# Finalizing the formula
cov = var5 / ((len(arg1)) - 1)
return cov
################################################################
def corr(arg1, arg2, df = False, pval = False):
## takes the formula = cov(x,y)/sd(x).sd(y)....
var1 = cov(arg1, arg2)
sd_x = sd(arg1)
sd_y = sd(arg2)
correlation = var1 / (sd_x * sd_y)
##
if df == True or pval == True:
Df = len(arg1) - 2
#pval =
return correlation
####################################################################################################################################################################
#P VALUE FOR CORRELATION ANALYSIS (ALPHA = 0.05)
####################################################################################################
def p_val(n, r):
''' Function calculates DF(degrees of freedom) from the total number of data points. It takes total number of data points(n) and pearson correlation cofficent(r) as an input and prints whether the altenrative hypothesis is rejected or accepted based on ALPHA = 0.05. P-Value is also printed to be < or > 0.05'''
# lists of DF and critical value of alpha are generated to produce ...
#...fast and less computationally expensive results.
p = [0.997, 0.950, 0.878, 0.811, 0.754, 0.707, 0.666, 0.632, 0.602, 0.576, 0.553, 0.532, 0.514, 0.497, 0.482, 0.468 , 0.456, 0.444, 0.433, 0.423, 0.413, 0.404, 0.396, 0.388, 0.381, 0.374, 0.367, 0.361, 0.355, 0.349, 0.325, 0.304, 0.288, 0.273, 0.250, 0.232, 0.217, 0.205, 0.195]
df_list = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 35, 40, 45, 50, 60, 70, 80, 90, 100]
# magnitude of correlation coefficent(r) is required, here we are not ...
#.. concerned with the direction (sign) of the coefficent.
r = abs(r)
# DF is n - 2 because the steps needed to arrive at coefficients from raw data are 2
df = n - 2
if df >= 100:
value = p[38]
else:
n = 0
for i in df_list:
if df == df_list[n]:
value = p[n]
elif df > df_list[n] and df < df_list[n+1]:
val = p[n]
else:
n = n + 1
if r >= value:
return 'P-Val < 0.05' + ', ' + str(df)
if r < value:
return 'P-Val > 0.05'+ ', ' + str(df)
##############################################################################
################################################################
######################################################################################################
#PROBABLE ERROR OF CORRELATION
######################################################################################################
import math
def PE(r, n):
'''This function calculates Probable Error(PE) it takes in correlation coefficeint(r) and total data points(n) as variables and returns a string of values seperated by commas. The string contains values of PE, Standard error(SE), Lower limit of rho, upper limit of rho, range of rho and df, in the same order.'''
SE = (1 - r**2) / (math.sqrt(n))
PE = 0.6745*SE
rho_lower = r + PE
rho_upper = r - PE
rho_diff = rho_lower - rho_upper
if r < PE:
u = 'r < Probable Error(PE); NO SIGNIFICANT CORRELATION EXISTS'
elif r >= 6*PE:
u = 'r >> Probable Error(PE); HIGHLY SIGNIFICANT CORRELATION EXISTS'
else:
u = 'r > Probable Error(PE); SIGNIFICANT CORRELATION EXISTS'
return str(PE) + ', ' + str(SE) +' ,' + str(rho_lower) + ', ' + str(rho_upper) + ', ' + str(rho_diff) + ', ' + str(u)
#################################################################
def concnest(*lists):
'''This function takes in multiple lists as arguments ('*' denotes multiple arguments can be given to the function) and returns a concatanated and nested parent list that contains entered lists as elements. 1st element of 1st list can be indexed as list[0][0].'''
nested_list = list(lists)
return nested_list
###############################################################
def newcor(arg1,arg2,truelist, headerlist):
''' This function is implemented so that, I don't have to re-write corr() function (Please refer to earlier posts). it takes 4 arguments. 'arg1' and 'arg2' are ints and they refer to elements of concatanated list between which a correlation is required. 'truelist' is that parent list. 'headerlist' is the list of headers of all elements. The function returns a comma-seperated-string with values of 'variables being correlated', 'correlation coefficient' , 'covariance', 'Probable Error', ' Standard Error', ' lower limit of rho(p)', ' upper limit of rho(p)', ' range of rho(p)', ' significance', ' P-value' , ' Df' '''
m_true = truelist[arg1]
n_true = truelist[arg2]
m_header = headerlist[arg1]
n_header = headerlist[arg2]
newcor_var = PE(corr(truelist[arg1],truelist[arg2]),len(truelist[arg1]))
pvalue = p_val(len(truelist[arg1]),corr(truelist[arg1],truelist[arg2]))
return str(m_header) +' VS '+ str(n_header) +', '+ str(corr(m_true,n_true)) + ', ' + str(cov(m_true,n_true)) + ', ' + str(newcor_var) + ', ' + pvalue + '\n'
################################################################
def corcovmatrix(parentlist):
''' this function takes a concatanated parent list (lists within a list) as an argument and returns a full correlation and covariance analysis along with probable and standard errors and p-values as a .csv file. A full analysis means all varaibles are combanitorically analysed with each other and a full report is generated as a .csv file or text'''
truelist = parentlist
csv_header = [' variables', ' Coefficent(r)', ' covariance', ' Probable Error', ' Standard Error', ' lower limit of rho(p)', ' upper limit of rho(p)', ' range of rho(p)', ' significance', ' P-value' , ' Df' ]
headerlist = []
n = 0
for i in truelist:
headerlist.append(truelist[n][0])
del truelist[n][0] # proper way of indexing list within a list is this ..
n = n + 1
lst1 = []
n = 0
for i in truelist[:len(truelist)-1]:
lst1.append(newcor(n,n+1,truelist,headerlist))
n = n + 1
lst2 = []
for i in range(len(truelist)-2):
j = len(truelist)-2
while j >= 0:
lst2.append(newcor(-1,j,truelist,headerlist))
j = j - 1
del truelist[-1]
del headerlist[-1]
final_header = ','.join(csv_header)
final_list = ''.join(lst1+lst2)
print(final_header)
print(final_list)




Comments